| One of the most asked questions in risk management has been: How much do you stand to lose, over a certain period and with a certain probability? The common answer to this question today is Value at Risk, a risk measure that expresses itself as one number. What is that number and what does it stands for? In order to interpret this number we first have to assume that: |
 |
- Everything assumed in the (VaR) calculations/process is true
- All approximations made are accurate
- The future follows the past and whatever risk you are analyzing only exists for the specified (certain) period
If you are reasonably comfortable with all of the above, then the one number to answer your question is Value at Risk: A worst case loss with limits on time period and probability.
This course takes an in-depth look at the calculation methodologies of the Value at Risk measure. We review Value at Risk (VaR) calculation methods in particular the Variance-covariance approach and the Historical simulation approach. We build a simple portfolio comprising of Euro, Australian dollar, Yen, GBP, Brent, WTI, Gold and Natural Gas and calculate VaR for the portfolio using both of these methodologies.
Course Prerequisites
Comfort with basic mathematics, statistics, probability and EXCEL and some familiarity with local markets and portfolio management.
Course Audience
The course is targeted towards intermediate and advanced users and is aimed primarily at individuals responsible for capital allocation, limit setting and risk management within banks, insurance companies, mutual funds, as well as finance departments of non-financial organizations who need to quickly review or refresh their understanding of VaR methodologies for work or personal development.
Course Guide
Here is the structure of the course.
|
|
|
|
| Session 1 – Theoretical Overview |
36:06 mins |
|
| Session 2 – VaR Qualifications |
23:39 mins |
|
| Session 3 – Calculating VaR for a single security using VCV and Historical Simulation approaches |
44:52 mins |
|
| Session 4 – Extending the VaR model to a portfolio. Calculating portfolio VaR without a VCV matrix |
33:00 mins |
|
| Session 5 – Value at risk for Fixed income securities – Rate and Price VaR; Delta and Full Valuation approaches |
10:00 mins |
|
We walk through the process of calculating VAR for currencies and commodities. We start will a simple data sheet comprising of 4 currencies. Step by step we construct an excel sheet that handles the calculation of value at risk for each currency under the variance covariance (VCV) and historical simulation approaches. In addition to this we :
- Calculate 10 – day Trailing volatility (minimum and maximum volatility) and its graphical representation which are useful for interpreting VAR results.
- Calculate Daily, annualized and holding period volatility
- Calculate a crude check of the worst case loss and VAR result using the maximum trailing volatility figure and the holding period and present an interpretation of the disconnect between this crude measure and the VCV VAR.
- Show how to install and use the in-built Histogram (Data Analysis) function of EXCEL to determine the worst case loss for the historical simulation approach.
- Compare the VAR results under both approaches.
- Extend the model to commodities including WTI, Brent, Gold, Silver and Natural Gas.
- Calculate Portfolio VaR using the Variance Covariance Matrix Multiplication approach as well as the portfolio return short cut.
- Compare the results of the two approaches
- Calculate VaR for Fixed Income Bonds and differentiate between Price VaR, Rate VaR and Delta Neutral approximation versus the full valuation approach for fixed income securities.
Session One – Theoretical Overview
|
| We take a detailed look at Value at Risk, VaR. We consider its various definitions and the questions that it may be used to answer. We see how the tool may be extended from its traditional market risk application to other applications such as margin management and profitability calculations. We consider how VaR is used to estimate capital for capital allocation purposes, marginal capital needed for additional investments made, to make comparisons of risk measures over time. We look at the general step-by-step process followed for calculating VaR and an introduction on the difference and uses between Rate VaR and Price VaR for calculating risk on Fixed Income securities. |
|
 View a sample of session one View a sample of session one |
Session Two: VaR Qualifications
|
| In this session we continue with our discussion of Value at Risk, VaR, starting with the difference between Price and Rate VaR. We move onto another VaR Case study which looks at the determination of VaR using the historical simulation approach. Next we review in detail the processes behind the calculation of each of the three VaR methods, issues with each method and comparisons between them. We see how the calculation is impacted for a change in the liquidation or holding period assumption. Lastly we look at Nicholas Nassim Talebs views on VaR in particular his rules for risk management. |
|
 View a sample of session two View a sample of session two |
Session Three: Calculating VaR for a single security using VCV and Historical Simulation approaches
|
| A detailed look at Value at Risk, VaR. We consider its various definitions and the questions that it may be used to answer. We see how the tool may be extended from its traditional market risk application to other applications such as margin management and profitability calculations. We consider how VaR is used to estimate capital for capital allocation purposes, marginal capital needed for additional investments made, to make comparisons of risk measures over time. We look at the general step-by-step process followed for calculating VaR and an introduction on the difference and uses between Rate VaR and Price VaR for calculating risk on Fixed Income securities. |
|
 View a sample of session three View a sample of session three |
Session Four: Extending the VaR model to a portfolio. Calculating portfolio VaR without a VCV matrix
|
| We extend the earlier discussion regarding VaR calculation for currencies to commodities. We then demonstrate how to calculate Value at Risk for a portfolio of securities using both the Variance Covariance (VCV) approach as well as the Historical Simulation Approach. We use a short cut method for the VCV approach that bypasses the need to construct a VCV matrix. However we also cross check the results from this short cut method with those obtained from the matrix method. During this course we demonstrate the use of EXCEL’s in-built TRANSPOSE and MMULT functions. |
|
 View a sample of session four View a sample of session four |
Session Five: Value at risk for Fixed income securities – Rate and Price VaR; Delta and Full Valuation approaches
|
| We consider its various definitions and the questions that it may be used to answer. We see how the tool may be extended from its traditional market risk application to other applications such as margin management and profitability calculations. We consider how VaR is used to estimate capital for capital allocation purposes, marginal capital needed for additional investments made, to make comparisons of risk measures over time. We look at the general step-by-step process followed for calculating VaR and an introduction on the difference and uses between Rate VaR and Price VaR for calculating risk on Fixed Income securities. |
|
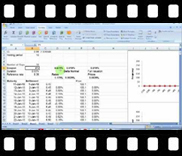 View a sample of session five View a sample of session five |
|
|
Back to top




